Bjørns ausgewählte Aufgaben

Definition: Die "iterierterte Quersumme" Y einer Zahl X sei die Wiederholung der Quersummenoperation, bis die Quersumme einstellig ist.

g Zahlenschloss

Ein Zahlenschloss hat 8 Zahlenringe, jeweils mit den Ziffern 1..9.
Die gesuchte Zahlenkombination kann als Zahl betrachtet werden.

In der gesuchten Zahl kommt jede Ziffer entweder mehrfach oder gar nicht vor, aber es stehen nie zwei gleiche Ziffern direkt hintereinander.
Die Zahl ist teilbar durch 55, aber nicht durch 25.
Die Quersumme ist 23.

Auswertung

Summiere die Elemente Ziffer Stelle i mal Ziffer Stelle (8-i+1) für i = 1..4.
Die Zielzahl g sei die iterierte Quersumme der Summe.

h Wiegen

Seien N Kugeln gegeben. Alle Kugeln wiegen dasselbe bis auf eine Kugel, die entweder leichter oder schwerer ist - man weiß es nicht.
Zum Wiegen steht eine Balkenwaage zur Verfügung, aber keine Gewichte.
Wie groß darf N maximal sein, um die abweichende Kugel festzustellen, wenn man 5 mal auf der Waage wiegen darf?

Auswertung

Die Zielzahl h ist die iterierte Quersumme von N.

i Advent

  ADVENT
+ ADVENT
= REZEPT

Auswertung

Die Zielzahl i sei die iterierte Quersumme von REZEPT.

j Schmaler Korridor

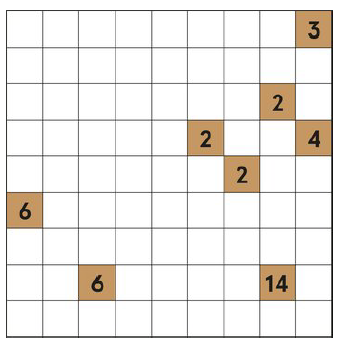Torsten hat einen unvollständigen Grundriss einer Etage bekommen. Auf dem Plan sind von den Räumen nur die Zellen mit den Eingangstüren verzeichnet und vermerkt, wie groß (in Zellen) die zugehörigen Räume groß sind. Die Zellen eines Raums sind immer über gemeinsame Kanten verbunden, aber niemals haben zwei Räume eine gemeinsame Kante. Über den Korridor, der alle Nicht-Raum-Zellen verbindet, kann man von jedem Raum zu jedem anderen Raum gelangen. Der Korridor ist überall so schmal, dass es keine freie Stelle gibt mit 2x2 Zellen.

Auswertung

Summiere die Multiplikationen von Anzahl Raumzellen Zeile i mal Anzahl Raumzellen Zeile (9- i+1) für i = 1..4. Die Zielzahl j sei die iterierte Quersumme der Summe.

k Bunt gemischt

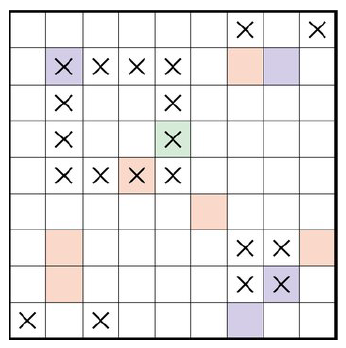Ein spezielles antikes 9x9 Webmuster erfordert, dass in jeder Webzeile und jeder Webspalte exakt drei mal jeweils die Farben Rot, Blau und Grün auftauchen. Leider sind von dem Muster nur noch wenige weitere Fakten überliefert. In dem Diagramm sind Zellen mit "x" markiert, wenn keine über eine Seite benachbarte Zelle die gleiche Farbe hat.

Auswertung

Summiere die Multiplikationen von Anzahl grüne Zellen mit Anzahl rote Zellen mit blaue Zellen für beide Diagonalen. Die Zielzahl k sei die iterierte Quersumme der Summe.

l Quadrate

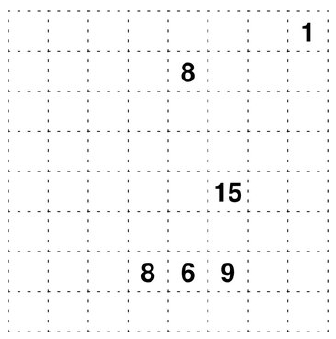Auf einem antiken Rechenkästchenpergament der Seitenlänge 8 aus Athen waren ursprünglich entlang der Linien einige Quadrate eingezeichnet. Nach der Überlieferung sollen sie keine gemeinsamen Ecken oder Kanten gehabt haben. Zur Rekonstruktion der verwitterten Quadrate dienen mühsam restaurierte Zahlen in einigen Zellen. Sie geben die Summe der Seitenlängen der Quadrate an, in denen sich die Zelle zur Zahl befindet.

Auswertung

Summiere die Flächengröße aller Quadrate (in Zellen). Die Zielzahl l sei die iterierte Quersumme der Summe.

m 5-Ecke

Sei N die Anzahl verschiedener flächengleicher konvexer 5-Ecke, die eine Ebene lückenlos und überlappungsfrei überdecken können. Beim Bedecken der Ebene dürfen beliebig Spiegel- und Drehsymmetrien des 5-Ecks mit verwendet werden, sie werden als das gleiche 5-Eck betrachtet. Zwei verschiedene 5-Ecke unterscheiden sich somit nur in den Verhältnissen der Innenwinkel und/oder Seiten.

Auswertung

Die Zielzahl l sei die iterierte Quersumme von N.

n Da lacht die TK

Setze den Witz wieder zusammen!

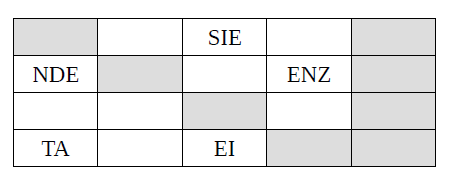
Auswertung

Die Zielzahl n sei die iterierte Quersumme der Summe aller grauen Felder.

o Pfeile

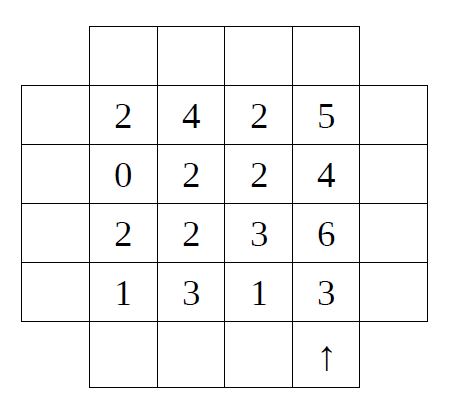Zeichne in jedes Feld am Rand einen Pfeil so ein, dass die Zahlen in den Feldern genau die Anzahl der Pfeile angibt, die auf diese Zahl zeigen.

Die Pfeile müssen immer auf mindestens eine Zahl zeigen und dürfen waagerecht, senkrecht oder im 45°-Winkel eingezeichnet werden. (Ein Pfeil als Vorgabe)

Auswertung

Zähle alle Pfeile, die nicht senkrecht auf das Nachbarfeld zeigen. Die Zielzahl o ist die iterierte Quersumme dieser Anzahl.

p Blockbildung

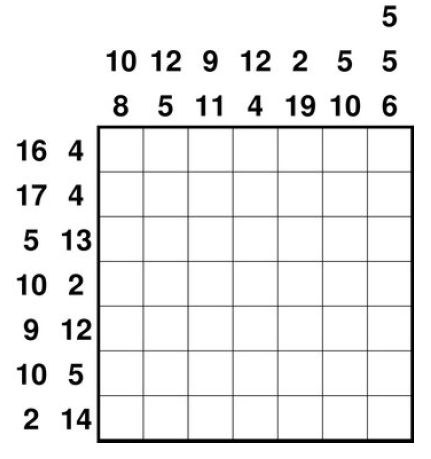In jeder Zeile und jeder Spalte dürfen die Zahlen 1..6 maximal einmal vorkommen. Die Zahlen am Rand geben die Summen der Zahlen von Gruppen direkt aufeinanderfolgender Zellen mit Zahlen an. Mehrere Gruppen in einer Zeile/Spalte sind durch eine oder mehrere schwarze Zellen (ohne Zahl) getrennt. Es können aber auch schwarze Zellen am Rand liegen.

Auswertung

Zähle alle schwarzen Zellen. Die Zielzahl p ist die iterierte Quersumme dieser Anzahl.

Weiter zur finalen Formel